在面对人生中存在的各种问题时,我们都希望可以做出合理的判断。但是问题来了,道理我们都知道,但实际操作时,我们又该如何用概率思维去指导决策?本篇文章里,作者就介绍了两种实用小技巧,或许会对你有所帮助。
正所谓“知易行难”,懂得道理固然重要,如何在面对各种各样的问题时灵活使用概率思维指导决策就显得尤为珍贵。
前言
上一篇《概率思维,人生真正的指南(上)》给大家介绍了基于概率思维决策的四种底层逻辑。大家明白了“选择大于努力”这句话,从概率的角度看是存在科学依据的。同样的机会,人生算法不同,结果也就不同。
正所谓“知易行难”,懂得道理固然重要,如何在面对各种各样的问题时灵活使用概率思维指导决策就显得尤为珍贵。
举个小例子,给你两个选择,选A就能赚10元,选B不赚钱,我相信绝大多数人肯定会选A。在这种情况下,我们之所以能做出正确决策的前提条件是掌握了决策所需要的全部信息,也就是完全信息决策。但在现实生活中我们面对的大多数决策都是“不完全信息决策”,我们没有足够的信息知道选A、选B有多大可能性赚到多少钱。在不完全信息决策的情况下,不是靠努力就一定能有正确决策的。
这篇文章,主要给大家介绍两种非常实用的实战小技巧。
一、概率对冲
为了帮助大家能够更好的理解什么是“概率对冲”,我们还是举个小例子。现在有两个按钮,按下红色按钮,你可以直接拿走1万元,按下绿色按钮,有一半机会,你可以拿到100万元,但还有一半机会,你什么都拿不到。你会选哪一个?

选择按红色按钮,落袋为安,宁愿收益小一点,但是收益确定。正所谓“二鸟在林,不如一鸟在手”,大部分人不愿为了看似更大的收益冒风险,他们更喜欢虽然小一点但是确定的收益,因此,“确定效应”就是他们的“人生算法”。或许大家认为,无论选择哪一种,只代表选择的风险偏好不同而已。但其实这道选择题,是有唯一正确答案的。那就是选择绿色按钮,因为绿色按钮的“期望值”更大(期望值为50万),是最理性的选择。
可是,有人会说,即便绿色按钮是最正确、最理性的选择,我还是有一半可能什么都拿不到啊,怎么办?
有没有一种办法,让我能确定地获得比1万元更大的收益呢?
答案当然是“有”。方法就是“概率对冲”。
让我们回到期望值本身……

所以,我们可以适当降低对应的奖励来提高概率,从而换取一个相对更高的期望值。那具体如何操作呢?
比如,我们可以找到一个风险投资机构,把这个项目以低于期望值50万的价格卖给他,比如20万,那么我就获得了确定性收益20万。但风投机构为什么愿意这么干呢?很简单,项目预期收益50万,而他只需要付出20万成本,因此他会有30万的预期收益。
从数学上看,基于期望值理论,选择绿色按钮是一个相对正确的决策。但在现实生活中,这个决策并不完美,依然有一定风险。这时我们就可以运用“概率对冲”思想,找到一些解决方案,尽可能降低概率的不确定性给我们带来的风险。这就是“概率对冲”思想的精髓。
二、多重先验
另外一种非常普遍的现象是,人们在对“可能性”进行预测时,往往要面对内心的问题:对自己做出的判断是否有信心。人不是机器,对自己做出的结论产生怀疑是非常正常的。实际上,我们进行选择时会经常问自己:“这个选择真的是正确的吗?”
比如,我们经常使用的“十有八九会是那样”的表述形式,就体现了“十成之中,有八九成会是那样”的一种预测。如果用概率来表示,就是“预计发生那件事的概率是80%~90%”。
如果认真思考一下,就会发现这种表述形式是非常奇怪的。之所以这么说,是因为概率本来就是由于无法做出确切判断,才不得不使用的不确切的表达方式。总体来说,概率给人的感觉就是“可能会发生,也可能不会发生”。在表述概率值时,如果再给出“80%~90%”的选择范围,就会进一步增加不确定性。这么做到底是为什么呢?
可以说,这正是“缺乏自信”的一种表现。在现实生活中,人们如果缺乏自信,就会准备多个备选答案。比如,“这可能是A干的,也可能是B干的”,“这部电影的口碑毁誉参半,有人认为很精彩,有人认为很无聊”等。一般来说,当缺乏做出明确判断的自信时,人们就会列举多种可能性。
因此,针对同一事件,人们在内心中往往会给出多个概率。也就是说,人们会分配多个数值,比如发生事件的概率“可能是80%,也可能是90%”。在专业术语中,这种适用多个概率模型的决策方式,被称为多重先验(multiple prior)。
从数学角度构建与多重先验相关的概率理论最早可以追溯到20世纪80年代。以色列数学家伊扎克·吉尔伯阿和大卫·施迈德勒最先提出这一理论,并在随后开展了大量相关研究。
针对心中拥有多重先验判断的人,伊扎克·吉尔伯阿和大卫·施迈德勒提出了一个设想,先是计算按照多个概率模型实施行动时的结果,也就是“收益期望值”,然后在此基础上运用“最大最小准则”进行决策。
比如某位决策者在面对从未处理过的复杂事件时,内心有两种截然不同的先验判断:第一种是“事件X成功的概率为0.7,失败的概率为0.3”;第二种是“事件X成功的概率为0.4,失败的概率为0.6”。对于事件X,需要投入60万元的成本,如果成功,可以获得100万元的回报,如果失败,将颗粒无收。如果你是这位决策者,你会去做这件事吗?
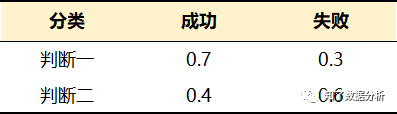
对此,伊扎克·吉尔伯阿和大卫·施迈德勒提出了一个方案,建议使用“期望值”和“最大最小准则”。首先,分别计算两种先验状态下的期望值,然后,从中选择较差的一方作为评估标准。
在这个案例中,我们在进行决策时,第一种先验判断的期望值为10万元(100万×0.7-60万),第二种先验判断的期望值为-20万元(100万×0.4-60万元)。应该选择两者之中较差的-20万元作为保底值。在这种情况下,不采取任何行动时的利润为0万元(保底值),大于采取行动时的保底值-20万元,由此可以判断,该决策者不应采取任何行动。
这种多重先验判断是在人们缺乏对未来进行预测的信心时产生的。伊扎克·吉尔伯阿和大卫·施迈德勒从数学角度固化了其运用机制。
自然形成多重先验并且发挥重要作用的就是医疗领域的“第二意见”。
“第二意见”是指除了主治医生以外,患者向其他医生咨询关于自身疾病治疗方针的建议。近年来,其重要性备受关注,成了讨论的焦点,逐渐被纳入普通的医疗体系,得到了广泛的应用。这种机制的优点非常明显:一方面,患者在选择自身疾病的治疗方案时,可以更广泛地征求意见,并充分发挥各种资源的作用;另一方面,主治医生可将确定治疗方案的部分责任交还给患者本人,从而减轻医生的责任负担。
这里有一点需要特别注意,当患者得到第二意见时,往往会产生多重先验判断,这是一个不可回避的事实。比如,主治医生认为“通过手术治愈这种疾病的概率为90%,通过用药治愈的概率为20%”。与之相对,给出第二意见的医生则认为“通过手术治愈这种疾病的概率为60%,通过用药治愈的概率为50%”。
在这种情况下,对于患者而言,作为治愈的概率模型,会产生两种先验判断:通过手术治愈的概率为90%,通过用药治愈的概率为20%;通过手术治愈的概率为60%,通过用药治愈的概率为50%。
然而,患者是难以对这两种先验判断进行优先级排序的。这是因为大多数患者本身并不具备医学专业知识,而提出上述概率模型的都是拥有医学专业知识的医生。患者缺乏充分的依据对两种先验判断进行比较,并选择自己应该信任的一方。
如果患者根据伊扎克·吉尔伯阿和大卫·施迈德勒提出的理论对“是否进行手术”做出选择,则具体判断过程如下:当选择手术作为治疗方案时,应该参照最差情况下的成功概率60%;当选择用药作为治疗方案时,应该参照最差情况下的成功概率20%。无论哪种情况,患者得到治愈的前景都不得不蒙上一层悲观色彩。面对这样的情况,患者恐怕只能选择将自己的命运交给手术治疗了。
那么,在我们的现实生活中,应该如何充分发挥它的作用呢?
多重先验理论发挥作用的途径主要有两个方面:一是平时积极培养利用多重先验理论进行思考的习惯;二是坚持认为人们是在多重先验理论的支配(不管有意还是无意)下实施行动的,并积极利用这一特点,充分发挥其在自己决策方面的作用。
人生其实就是一个不断决策的过程,我们生活中的每个瞬间都离不开一系列的连续决策。有些人总是试图逃避决策,但是大家不要忘记一点,“逃避”这种行为本身也是一种决策。也就是说,我们是无法绝对回避决策的。当我们不得不面对人生的各种问题时,希望这两篇文章能够给大家一点点启发。
微信公众号:知了数据分析
本文由 @知了数据分析 原创发布于知识吧。未经许可,禁止转载。
题图来自Unsplash,基于CC0协议。
